GGC

11. Sequences, Recursive Definitions, and Induction

11.1. Sequences, Series, and Sigma Notation

11.1.1. Sequences

A sequence is a function from the natural numbers \(\mathbb{N}=1,2,3\ldots\), into a set \(A\). The sequence may be denoted \(a_n\) for the sequence \(a_1,\ a_2,\ldots\). Sometimes the domain of the sequence may be the set of nonnegative numbers, \(0,1,2,3\ldots\), in which case \(a_n\) would be the sequence \(a_0,\ a_1,\ a_2,\ldots\).

Sequences may be defined using explicit functions or may be defined recursively.

Example 1

The sequence \(a_n=f(n)=3n+1\) is the sequence generated by the linear function \(f(x)=3x+1\), whose first 5 terms would be

\(a_1=\ 3\left(1\right)+1=4\)

\(a_2=3\left(2\right)+1=7\)

\(a_3=3\left(3\right)+1=10\)

\(a_4=3\left(4\right)+1=13\)

\(a_5=3\left(5\right)+1=16\)

The same sequence may be defined recursively as \(a_1=4\) and \(a_n=a_{n-1}+3\). So

\(a_1 = 4\)

\(a_2=a_{2-1}+3=a_1+3=4+3=7\)

\(a_3=a_{3-1}+3=a_2+3=7+3=10\)

\(a_4=a_{4-1}+3=a_3+3=10+3=13\)

\(a_5=a_{5-1}+3=a_4+3=13+3=16\)

GGC

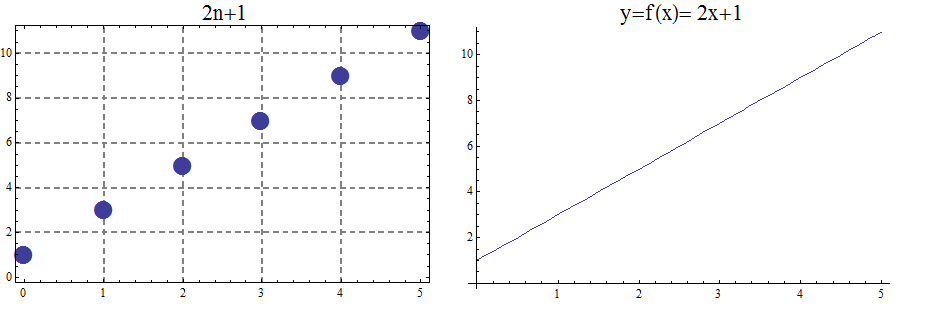
Sequences generated by linear functions as in Example 1 are called arithmetic sequences . Thinking recursively, they are determined by a first term and a common difference. The arithmetic sequence \(a_n=3n+1\) is the sequence whose first term is \(a_1=4\), and whose common difference is \(d=3\). As arithmetic sequences are generated by linear functions \(f\left(x\right)=dx+c\), the general arithmetic sequence is \(a_n=d\cdot n+b\), \(d\) being the common difference.

Example 2 - Possible to make a PYTHON TUTOR

The sequence \(b_n=f\left(n\right)=2\cdot\ 3^n\) is the sequence generated by the exponential function \(f\left(x\right)=2\cdot3^x\), whose first few terms would be

\(b_1=2\cdot\ 3^1=6\)

\(b_2=2\cdot\ 3^2=18\)

\(b_3=2\cdot\ 3^3=54\)

\(b_4=2\cdot\ 3^4=162\)

The same sequence may be defined recursively as \(b_1=6\), and \(b_n=3\cdot b_{n-1}\). So, \(b_2=3\cdot b_{2-1}=3\cdot6=18\)

\(b_3=3\cdot b_{3-1}=3\cdot18=54\)

\(b_4=3\cdot b_{3-1}=3\cdot54=162\)

GGC

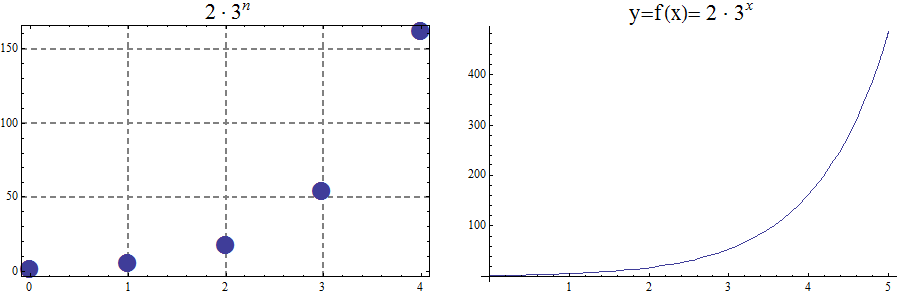
Sequences generated by exponential functions as in Example 2 are called geometric sequences . Thinking recursively, they are determined by a first term and a common ratio. The geometric sequence \(b_n=2\cdot3^n\), is the sequence whose first term is \(b_1=6\) and whose common ratio is \(r=3\). As geometric sequences are generated by exponential functions \(f\left(x\right)=a\cdot r^n\), the general geometric sequence is \( a_n=a\cdot r^n\), with \(r\) being the common ratio.

11.1.2. Series and Sigma notation

Given a sequence of numbers \( \left\{a_{n\ }\right\}=\left\{a_1,a_2,a_3,\ldots\right\}\) we are often interested in adding them up.

Adding a sequence of numbers produces what is called a series .

\( a_1+a_2+a_3+a_4\) is a finite series with 4 terms, and \( a_1+a_2+a_3+\ldots+a_n\) is a finite series up to some finite, but possibly variable number of terms \(n\).

By contrast \(a_1+a_2+a_3+\ldots\) is used to denote an infinite series .

There is a shorthand way of writing a series using sigma , or sum notation , denoted by the \(\sum\) symbol.

For example, \(a_1+a_2+a_3+a_4=\sum\limits_{i=1}^{4}a_i \) which means starting at \(i=1\), we add up \(a_1\) and then increase \(i\) to 2 and add \(a_2\), and so on, all the way up to the last one at \(i=4\).

\(a_1+a_2+a_3+\ldots+a_n=\sum\limits_{i=1}^{n}a_i\)

The infinite sum is denoted \(a_1+a_2+a_3+\ldots=\sum\limits_{i=1}^{\ \infty\ }a_i\)

Example 3

Consider \({a_n}=\left\{3n+1\right\}\)

\(\sum\limits_{i=1}^{4}a_i=a_1+a_2+a_3+a_4\)

\(=\left(3\times1+1\right)+\left(3\times2+1\right)+\left(3\times3+1\right)+\left(3\times4+1\right)=\sum\limits_{i}^{4}{(3i+1)}\)

\( \sum\limits_{i=1}^{n}a_i = a_1+a_2+a_3+\ldots+a_n\) \(=\left(3\times1+1\right)+\left(3\times2+1\right)+\left(3\times3+1\right)+\ldots +\left(3\times n+1\right)=\sum\limits_{i}^{n}{(3i+1)}\)

\(\sum\limits_{i=1}^{\ \infty\ }a_i=a_1+a_2+a_3+\ldots\) \(=\left(3 \times 1+1\right)+\left(3\times 2+1\right)+\left(3\times 3+1\right)+\ldots\ =\sum\limits_{i=1}^{\ \infty\ }{(3i+1)}\)

11.2. Defining Sequences Recursively

A recurrence relation for a sequence \({a_n}\) is an equation that expresses \(a_n\) in terms of one or more of the previous terms of the sequence, namely \(a_0, a_1, \dots, a_{n-1}\) for all integers \(n\) with \(n \ge n_0\), where \(n_0\) is a nonnegative integer. The initial conditions for such a recurrence relation specify the terms that precede the first term where the recurrence relation takes effect.

Example 4

Let \({a_n}\) be a sequence that sastifies the recurence relation \(a_n=a_{n-1}+na_{n-2}+1\) for \(n=2, 3,4, \dots\) and suppose that \(a_0=1\) and \(a_1=2\). Find \(a_2, a_3,\) and \(a_4.\)

Solution:

\begin{array}{lcl} a_2 & = & a_1 + 2a_0 + 1\\ &=& 2 + 2(1) + 1\\ a_2 &=& 5 \end{array}

\begin{array}{lcl} a_3 &=& a_2 + 3a_1 + 1\\ &=& 5 + 3(2) + 1\\ a_3&=& 12 \end{array}

\begin{array}{lcl} a_4 &=& a_3 + 4a_2 + 1\\ &=& 12 + 4(5) +1\\ a_4 &=& 33 \end{array}

Some sequences, like the Fibonacci sequence , are easier to generate recursively. The Fibonacci sequence is defined recursively as

\(f_1=1\) and \(f_2=1\), and \(f_n=f_{n-1}+f_{n-2}\).

So, \( f_3=f_{3-1}+f_{3-2}=f_2+f_1=1+1=2\)

\(f_4=f_{4-1}+f_{4-2}=f_3+f_2=2+1=3\)

\(f_5=f_{5-1}+f_{5-2}=f_4+f_3=3+2=5\)

\(f_6=f_{6-1}+f_{6-2}=f_5+f_4=5+3=8\)

\(f_7=f_{7-1}+f_{7-2}=f_6+f_5=8+5=13\)

Example 5

Find the first 6 terms of the sequence \(c_k=\frac{1}{k^2}\) generated by the function \(f(x)=\frac{1}{x^2}\).

Solution

\(c_1=f\left(1\right)=\frac{1}{1^2}=1\)

\(c_2=f\left(2\right)=\frac{1}{2^2}=\frac{1}{4}\)

\(c_3=f\left(3\right)=\frac{1}{3^2}=\frac{1}{9}\)

\(c_4=f\left(4\right)=\frac{1}{4^2}=\frac{1}{16}\)

\(c_5=f\left(5\right)=\frac{1}{5^2}=\frac{1}{25}\)

\(c_6=f\left(6\right)=\frac{1}{6^2}=\frac{1}{36}\)

GGC

We say we have solved the recurrence relation together with the initial conditions when we find an explicit formula, called a closed formula , for the terms of the sequence.

Example 6

Determine whether the sequence \({a_n}\) where \(a_n=2^n\) for every nonnegative integer \(n\) is a solution of the recurrence relation \(a_n=2a_{n-1}-a_{n-2}\) for \(n=2, 3, 4, \ldots\).

Solution:

Using the equation \(a_0=2^0=1\), \(a_1=2^1=2\), and \(a_2=2^2=4\). Because \(a_2=a_1-a_0=2*2-1=3\) and this is not the value of \(a_2\), we say that \({a_n}\) where \(a_n=2^n\) is not a solution (or closed formula) for the recurrence relation.

We can solve a recurrence relation using iteration .

Example 7

Solve the recurrence relation \(a_n=a_{n-1}+3\) when \(a_1=2\).

Solution:

We are looking for a closed formula, so we will successively apply the recurrence relation until we see a pattern. \begin{align*} a_2&=a_1+3=2+3\\ a_3&=a_2+3=(2+3)+3 =2+3\cdot 2\\ a_4&=a_3+3=(2+2\cdot 3)+3=2+3\cdot 3\\ \vdots\\ a_n&=a_{n-1}+3=(2+3(n-2))+3=2+3(n-1)\\ \end{align*} So our closed formula is \(a_n=2+3(n-1)\).

A recursively defined function has two parts:

  • BASIS STEP: Specify the value of the function at zero

  • RECURSIVE STEP: Give a rule for finding its value at an integer from its value at smaller integers.

This is similar to a recurrence relation, but using function notation.

Example 8

Consider again the Fibonacci numbers , but this time given by a function \(f(n)\) where \(f(0)=0\), \(f(1)=1\) and for \(n \geq 2\) \(\)f(n)=f(n-1)+f(n-2)\(\)

Applying the formula gives \begin{align*} f(2)&=f(1)+f(0)=1+0=1\\ f(3)&=f(2)+f(1)=1+1=2\\ f(4)&=f(3)+f(2)=2+1=3\\ f(5)&=f(4)+f(3)=3+2=5\\ f(6)&=f(5)+f(4)=5+3=8\\ \end{align*} Thinking of this as a recurrence relation we would write \(f_0=0, f_1=1\) and \(f_n=f_{n-1}+f_{n-2}\). Generating the sequence \({0,1,1,2,3,5,8,\ldots}\).

11.3. Recursive Algorithms

Algorithms or procedures may invoke other procedures. An algorithm that calls itself is said to be a recursive algorithm .

One way to think of recursive algorithms, is as algorithms which reduce tasks to instances of the same task with a smaller number of inputs.

We illustrate with some basic examples. The first few examples are intended mainly to introduce the concept of recursion and are not necessarily the most efficient or intuitive ways to implement the given tasks. Recursive methods are to be contrasted with iterative methods.

11.3.1. Recursive Implementation of Factorial

We begin with a recursive method for computing \(n!\) for integers \(n \geq 0\).

Recall that \(5!=5\ \times\ 4\ \times\ 3\ \times\ 2\ \times\ 1\ =\ 5\ \times\ 4!\).

In general, we may define \(n!\) recursively or inductively as

\(0!=1\)

\(n!\ =\ n\ \cdot\ (n-1)!\ \)

An implementation of the factorial procedure is given below.

Table 4. Factorial \(n!\) in Pseudocode
Recursive Iterative 
procedure factorial(n)
begin
	if n equals 0 then
		return 1
	else
		return  n * factorial(n-1)
	end if
end
 
procedure factorial(n)
begin
	z = 1
	for i = 1 to n do
		z = z * i
	return z
end
Example 10 - Recursive Implementation of Factorial Function, \(n!\), in Python

The Python code below implements the factorial function \(n!\) recursively.

11.3.2. Recursive Implementation of the Power Function \(b^n\)

As another simple example, we consider a recursive implementation of exponentiation \(b^n\) with \(n\) a nonnegative integer, \(b>0\), and \(b \neq 1\).

Consider for example \(5^4=5\ {\cdot\ 5}^3\) Hence we can recursively define exponentiation as

\(b^0=1\)

\(b^n=b\cdot\ b^{n-1}\).

A pseudocode recursive implementation of the power function or exponential function \(b^n\) is below.

Table 5. Power Function \(b^n\) in Pseudocode
Recursive Iterative 
procedure exponentiation(b, n)
begin
	if n equals 0 then
		return 1
	else
		return  b * exponentiation(n-1)
	end if
end
 
procedure exponentiation(b, n)
begin
	z = 1
	for i = 1 to n do
		z = z * b
	return z
end

11.3.3. Recursively Defined Arithmetic Sequences

Consider the arithmetic sequence, \(5, 9, 13, 17,\ldots \), which is an arithmetic sequence with first term \(a_1=5\) and common difference \(d=4\), which may be defined recursively as

\(a_1=5\)

\(a_n=4+a_{n-1}\)

The general arithmetic sequence with first term \(a_1=a\) and common difference \(d\) can be defined recursively,

\(a_1=a\)

\(a_n=d+a_{n-1}\),

and the sequence can be generated recursively using the following pseudocode.

Recursive implementation of arithmetic sequences with first term \(a_1=a\), and common difference \(d\). 
procedure arithmetic(n, a, d)
begin
	if n equals 1 then
		return a
	else
		return d + arithmetic(n – 1, a, d)
end

11.3.4. Recursive Generation of the Fibonacci sequence

Recall the Fibonacci sequence \(1, 1, 2, 3, 5, 8, 13 \ldots \) is defined recursively,

\(f_1=1\)

\(f_2=1\)

\(f_n=f_{n-1}+f_{n-2}\)

We provide a recursive Python implementation to compute the \(n^{th}\) Fibonacci number.

Example 11 - Recursive Implementation of Fibonacci in Python

The Python code below uses the recursive relationship \(f_n = f_{n-1}+f_{n-2}\), to calculate the \(n^{th}\) Fibonacci number.

11.3.5. The Merge Sort Algorithm

Merge Sort is a recursive sorting algorithm. The general idea is to divide a list of length \(n\) into \(n\) sublists of length \(1\), where a list of length one is considered already sorted. Subsequently, the algorithm repeatedly merges the sublists to make sorted lists until only a single list of length \(n\) is remaining. This will be the a sorted list consisting of the elements of the original list.

The picture below illustrates this with a list of length seven.

GGC
Figure 12. Illustration of Merge Sort courtesy of Wikipedia
Example 12 - The Merge Sort Algorithm in Python

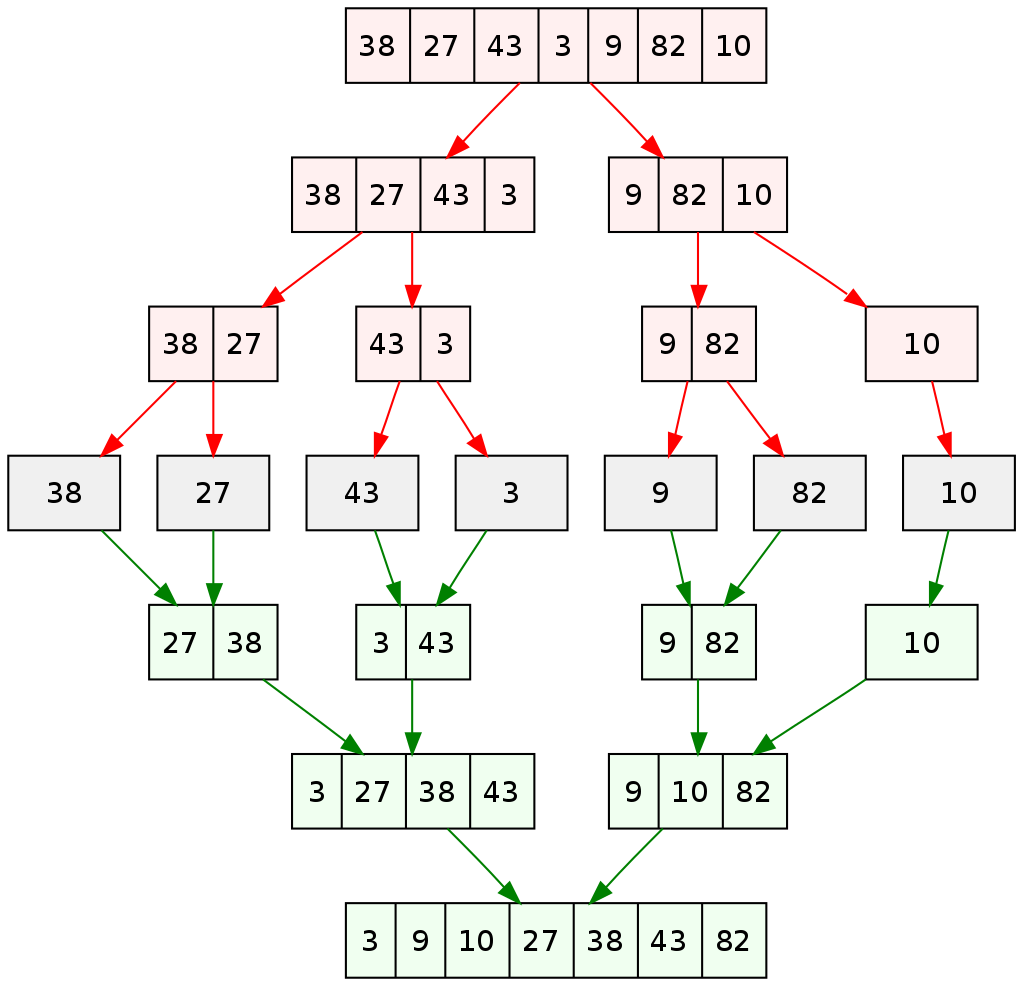
Notice that Merge Sort has complexity \(n \log{n}\). The first part of Merge Sort, similar to Binary Search which is \(O(\log{n})\), the list is repeatedly divides into two halves. The second part of Merge Sort merges \(n\) elements which occurs with complexity \(n\). Since the algorithm performs the first AND the second parts, we multiply to obtain that the complexity is \(O(n \log{n})\).

11.4. Mathematical Induction

Mathematical induction is a method of proof used to prove a series of different propositions, say \(P_1,\ P_2,P_3,\ldots P_n\). A useful analogy to help think about mathematical induction is that of climbing a ladder. It is useful to think of climbing a ladder as made up of two parts. The first part involves being able to actually step onto the ladder, or make it to the first rung (or at least some rung) of the ladder. The second part involves knowing that if we are on on some rung of the ladder we can get to the next rung of the ladder. This tells me I can climb the ladder.

GGC

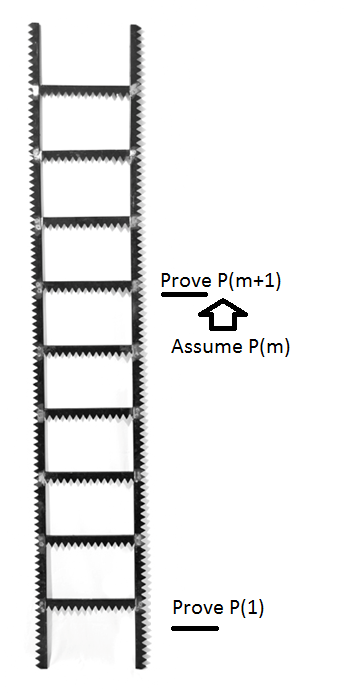
Remember to climb the ladder we require two different components.

  • I can get to the first step of the ladder or be able to prove that \(P(1)\) is true. This is called the basis step .

  • In the second component, I want to know that if I’m on any given step I can climb to the next one. Proving \(P(m+1)\) assuming \(P(m)\) for general \(m\), is called the induction step .

Example 9 - Proof by Induction

\(\)\sum\limits_{i=1}^{n}i=1+2+…​+n=\frac{n\left(n+1\right)}{2}\(\)

This is a sequence of statements in terms of \(n\) telling me that the sum of the first \(n\) integers is going be equal to some formula that depends on the final number \(n\) that you want to add.

Solution

Basis Step: When \(n=1\), there is only 1 term to add. Does \(1 \overset{?}{=}\frac{1\ \left(1+1\right)}{2}\)?

Since \(1=\frac{2}{2}\), this formula is valid when \(n=1\).

It also checks out when \(n=2\). \(1+2=\frac{2\ \left(2+1\right)}{2}\)

We may continue with \(n=3, n=4, ….\), etc., and notice that we want to prove an infinite collection of propositions. Specifically, we want to establish this claim for every positive integer.

Inductive Step: Assume the statement is true for \(P(m)\).

That is \(\sum\limits_{i=1}^{m}i=1+2+...+m=\frac{m\left(m+1\right)}{2}\) (called the inductive hypothesis).

Prove that this implies \(P(m+1)\) is true. That is show \(\sum\limits_{i=1}^{m+1}i=1+2+...+m+(m+1)=\frac{(m+1)\left(m+1+1\right)}{2}=\frac{(m+1)\left(m+2\right)}{2}\)

Begin with the left side \(1+2+...+m+(m+1)\)

We can rewrite this as \(\frac{m\left(m+1\right)}{2}+(m+1)\) using the induction hypothesis.

Now we simplify this using algebra and show that it is the same as the right hand side.

Factoring out \((m+1)\) gives,

\(\left(m+1\right)\left(\frac{m}{2}+1\right)=\left(m+1\right)\left(\frac{m}{2}+\frac{2}{2}\right)=\left(m+1\right)\left(\frac{m+2}{2}\right)=\frac{\left(m+1\right)\left(m+2\right)}{2}\)

Which is the same as the right-hand side!

So \(1+2+...+m+(m+1)=\frac{\left(m+1\right)\left(m+2\right)}{2}\), which means we have shown \(P(m+1)\) follows from \(P(m)\).

So, by induction, \(\sum\limits_{i=1}^{n}i=1+2+...+n=\frac{n\left(n+1\right)}{2}\) for all positive integers \(n\).

Types of statements that can be proven by induction:

  • Summation formulas: Prove that 1(1!) + 2(2!) + · · · + n(n!) = (n + 1)! – 1, for all positive integers.

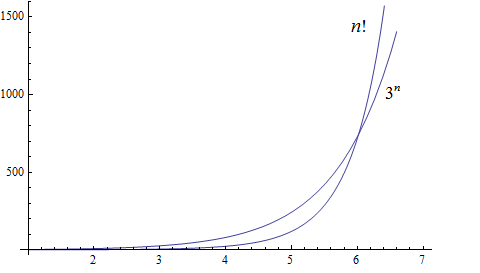
  • Inequalities: Prove that \(2^n < n!\) for every positive integer \(n\) with \(n ≥ 4\).

  • Divisibility: Prove that \(n^3+2n\) is divisible by 3 for every positive integer \(n\).

  • Sets: Prove that if \(S\) is a set with \(n\) elements where \(n\) is a nonnegative integer, then \(S\) has \(2^n\) subsets.

  • Algorithms: Prove that the recursively defined algorithm fac(n) returns \(n!\) for all nonnegative integers.

def fac(n) 

begin
if n = 0 then
return 1
else
return n · fac(n − 1)

end

Example 10 - A Summation Formula

Prove by mathematical induction \(1·1!+2·2!+3·3!+···+n· n!=\underset{k=1}{\overset{n}{\sum }}k\left( k!\right) =\left(n+1\right)!-1\)

Solution:

For each integer \(n\), let \(P(n)\) be the statement \(P(n):\sum\limits_{k=1}^{n} k\left( k!\right) =\left(n+1\right)!-1\)

To prove using induction we need

  • Base case: \(P(1)\) is true

  • Inductive step: For all integers \(m>0\), if \(P(m)\) is true, then \(P(m+1)\) is true.

Base Case: Substitute \(n=1\) into \( \sum\limits_{k=1}^{n}k(k!)=\left(n+1\right)!-1\)

\( \sum\limits_{k=1}^{1} (k)k!\overset{?}{=}\left(1+1\right)!-1\)

Simplify both sides to check for validity: 1==1, therefore the base case is true.

Begin the inductive step by assuming P(m) for some integer m>0.

Assume \(P(m):\sum\limits_{k=1}^{m}k(k!)=\left(m+1\right)!-1\) for some integer m>0.

Write down the left hand side of P(m+1):

\(P(m+1):\sum\limits_{k=1}^{m+1}k(k!)\)

Extract (m+1) (m+1)! from the summation,

\(\sum\limits_{k=1}^{m+1} k(k!)=\sum\limits_{k=1}^{m}kk!+(m+1)!(m+1)\)

Apply the induction hypothesis by replacing \(\sum\limits_{k=1}^{m}k(k!)\) with (m+1)!-1,

\(\sum\limits_{k=1}^{m+1}k(k!)=((m+1)!-1)+(m+1)!(m+1)\)

Simplify the result:

\(\sum\limits_{k=1}^{m+1}k(k!)=-1+2\left(m+1\right)!+\left(m+1\right)!m\)

\(=-1\ +(m+1)(2+m)=(m+2)!\ -1\ =((m+1)+1)!-1\)

Express the result in terms of m+1,

\(\sum\limits_{k=1}^{m+1}k(k!)=((m+1)+1)!-1\)

Therefore, the inductive step has been verified \(\sum\limits_{k=1}^{m+1}k(k!)=((m+1)+1)!-1\)

Example 11 - Another Summation Formula

Prove the proposition that the sum of the first n odd numbers is \(n^2\); that is,

\(1+3+5+···+2n-1=\sum_{k=1}^{n} (2k-1) =n^2\) for n a positive integer \(n\in\mathbb{Z}\)

Solution:

For each integer n, let P(n) be the statement \(\sum_{k=1}^{n} \left(2k-1 \right)=n^2\) \(P\left(n\right):\sum_{k=1}^{n} \left(2k-1 \right)=n^2\)

Base case: P(1) is true.

Inductive step: For all integers m>0, if P(m) is true, then P(m+1) is true. If the above properties hold, then for each n\(\in\mathbb{Z}\) where n>0, the statement P(n) is true.

Substitute n=1 into \(\sum_{k=1}^{n} (2k-1)=n^2\)

\(\ \sum_{k=1}^{1} (2k-1)\overset{?}{=}1^2 \)

Simplify both sides to check for validity:

1=1, therefore the base case is true and the inductive step can be taken.

Begin the inductive step by assuming \(P(m)\) for some integer \(m>0\). Assume for some integer m>0

\(P(m):\ \sum_{k=1}^{m} (2k-1)=m^2\)

Write down the left-hand side of \(P(m+1)\):

\(\text{LHS } P(m+1):\ \sum_{k=1}^{m+1}{(2k-1)}\)

Extract \( (m+1)-1\) from the summation,

\(\sum_{k=1}^{m+1} (2k-1)=\sum_{k=1}^{m}{(2k-1)}+(2(m+1)-1)\)

Apply the induction hypothesis by replacing \(\sum_{k=1}^{m}{(2k-1)}\), with \(m^2\).

\(\sum_{k=1}^{m+1} \left(2k-1\right)=m^2 +(2(m+1)-1)=m^2+2m+2-1\)

\(=m^2+2m+2\ =m^2 +2m+2(m+1)^2\)

Simplify the result expressing in terms of \(m+1\):

\(\sum_{k=1}^{m+1} {(2k-1)}={(m+1)}^2\).

In other words, \(\sum_{k=1}^{m} {(2k-1)}=m^2\), implies \(\sum_{k=1}^{m+1} {(2k-1)}=(m+1)^2\).

Therefore, the inductive step has been verified.

Example 12 - Inequality

Prove that \(n! > 3^n\) for every positive integer \(n\) with \(n > 6\).

Solution:

Since the base case value must be greater than 6, the base case value will be set to the next integer after 6, \(n=7\).

Does \(7!\overset{?}{=}3^7\)?

Simplify both sides to check for validity: \(5040>2187\), therefore the base case is true and the inductive step can be taken.

Begin the inductive step by assuming P(m) for some integer m>6. Assume,

\(P(m):\ m!>3^m,\) for some integer m>6.

We want to show this implies P(m+1) or,

\(P(m+1):\ (m+1)!>3^{m+1}\).

Write down the left hand side of

\(\text{LHS } \ P(m+1) : (m+1)!\)

Factor out \(m+1\) from \((m+1)!\):

\((m+1)!=m! (m+1)\)

Using the induction hypothesis \( m!>3^m\), then

\( m!(m+1)>3^m(m+1)\),

\(\left(m+1\right)!>3^m\left(m+1\right)\),

Using \(m+1>3\), then

\(3^m (m+1)>3^m3\)

Combining exponents, \(3^m 3=3^{m+1}\)

\((m+1)!>3^{m+1}\)

\(m!>3^m\) implies \((m+1 )!>3^{m+1}\).

induction3
Figure 13. Graphs of \(n!\), and \(3^n\), showing \(n! > 3^n\), for \(n>6\).
Example 13 - Divisibility

Prove the following using the principle of mathematical induction:

\(n^2 + n\) is even (or divisible by 2), for \(n > 0\).

Solution:

Since the base case value must be greater than 0, the base case value will be set to the next integer after 0: \(n=1\). For each integer \(n\), let \(P(n)\) be the statement \(n^2 + n\) is divisible by 2.

\(n^2+n\) is divisible by 2 if and only if \(\left(n^2+n\right)\mod 2=0\).

Prove \(\left(n^2+n\right)\mod 2=0\), for \(n>0\).

Substitute \(n = 1\) into \(\left(n^2+n\right)\mod 2=0\):

\((1^2 + 1) \mod 2 \overset{?}{=}0\)

Simplify both sides to check for validity:

\(2 \mod 2 = 0\), therefore the base case is true and the inductive step can be taken.

Begin the inductive step by assuming \(P(m)\) for some integer \(m > 0\):

Assume \(P(m):\ \left(m^2+km\right)\mod 2=0\) for some integer \(m>0\). Write down the left hand side of P(m+1):

\(\text{LHS }\ P(m+1):\ \left(m+1\right)^2+\left(m+1\right)\)

Expand \(\left(m+1\right)^2+\left(m+1\right)=m^2+2m+m+2\) and isolate \(m^2+m\) as its own term:

\((m+1)^2+(m+1)=\left(m^2+m\right)+\left(2m+2\right)\)

Factor 2 from \(2m+2\): \( \left(m^2+m\right)+2\ \left(m+1\right)\).

The induction hypothesis states that \(m^2+m\) is divisible by 2: \(\left(m^2+m\right)\mod 2=0\), and \(2 (m+1)\) has 2 as a factor explicitly, so

\(\left(2\left(m+1\right)\right)\mod 2=0\) and \(\left(m^2+m\right)\mod 2=0\) implies

\(\left((m+1)^2+(m+1)\right)\mod 2=0\)

Therefore, the inductive step has been verified.

11.5. Strong Induction

Recall the idea behind mathematical induction, prove that a proposition \(P\left(m\right)\) is true for a base step, say \(P_1\). Then prove the inductive step. This involves proving that \(P_m\) implies \(P_{m+1}\). Strong induction is a generalized version of induction where in the inductive step we assume \(P_1, P_2,\ldots, P_m\) is true and show all these together imply \(P_{m+1}\) is true.

Strong version of Mathematical Induction:

  • Base Case: Prove the first statement \(P_1\). (Or the first several \(P_r\), if needed.)

  • Inductive Step: Given any integer \(m \geq 1\), prove \(P_1\land {P_2\land {\ P_3\land {\ldots\land {P_m,\ }}}}\) implies \(P_{m+1}\)

Algorithmically:

  • Base Case: Prove that \(P_{1,\ }P_2\ ,\ldots,\ P_r\), are all true.

  • Inductive Hypotheses: Assume, \(P_{1,\ }P_2\ ,\ldots,\ P_m\)are all true for some \(m ≥ 1\),

  • Inductive step: Assuming, \(P_{1,\ }P_2\ ,\ldots,\ P_m\) are all true for some \( m ≥ 1\), prove that \(P_{m+1}\) is true.

Example 14 - Recurrence Relations

Consider the sequence \(\left\{a_n\right\}\) defined as a a recurrence relation,

\(a_1=5\), \(a_2=13\), and \(a_{n+2}=5a_{n+1}-6a_n\), for all \(n \geq 1\).

Prove that \(a_n=2^{n} +3^{n}\).

Solution

Base case: Consider the case \(n=1\), \(a_1=5=2^{1} +3^{1}\), and \(a_2=13=2^2 +3^2=4+9\).

Induction hypothesis: Assume \(a_1,\ a_2,..a_m\) are all given by \(a_m=2^m + 3^m\).

We want to show that \(a_{m+1}=2^{m+1} +3^{m+1}\).

Well, \( a_{m+1}=5a_m-6a_{m-1}\), using the definition of the recurrence relation.

By the inductive hypothesis, \(a_m=2^m+3^m\) and \(a_{m-1}=2^{m-1} +3^{m-1}\).

\( a_{m+1}=5\left(2^m +3^m \right)-6\left(2^{m-1} +3^{m-1}\right)\).

Consider then,

\[\begin{split} 5\left(2^m+ 3^m \right)-6\left(2^{m-1} +3^{m-1}\right) &=5\times 2^m +5\times 3^m -6\times 2^{m-1} -6\times 3^{m-1}\\ &=5\times 2^m+5\times 3^m-3\times 2\times 2^{m-1}-2\times 3\times 3^{m-1}\\ &=5\times\ 2^m+5\times 3^m-3{\times 2}^m-2\times 3^m\\ &=\left( 5\times 2^m-3\times 2^m \right) + \left( 5 \times 3^m -2\times 3^m \right)\\ &=\left(5-3\right) \times 2^m + \left(5-2\right) \times 3^m\\ &=2\times\ 2^m+3\times 3^m\\ &=2^{m+1} + 3^{m+1} \end{split}\]

So \(a_{m+1}=2^{m+1} + 3^{m+1}\) and therefore, \(a_n=2^n +3^n\) for all \(n \geq 1\).

11.6. Exercises

Prove using induction.

  1. For all \(n ≥ 1\) prove that \(1+2+3+\ldots+n=\displaystyle\sum_{i=1}^{n}i=\displaystyle \frac{n\left(n+1\right)}{2}\)

  2. For all \(n ≥ 1\) prove that \(1^2+2^2+3^2+\ldots+n^2=\displaystyle\sum_{i=1}^{n}i^2=\frac{1}{6} n (n+1) (2 n+1)\)

  3. For all \(n ≥ 1\) prove that \(1^3+2^3+3^3+\ldots+n^3=\displaystyle\sum_{k=1}^{n}k^3=\frac{1}{4} n^2 (n+1)^2\)

  4. For all \(n ≥ 1\), prove that \({23}^n-1\) is divisible by 11.

  5. Prove by induction that \(n^2+n = n(n+1)\) is even for all integers \(n ≥ 1\).

  6. Find an appropriate \(N \in \mathbb{Z}\), and prove by induction that \(n^3 +3n^2\) is even for all \(n ≥ N\).

  7. Find an appropriate \(N \in \mathbb{Z}\), and prove by induction that \(n^3 +2n\) is divisible by 3 for all \(n ≥ N\). (Hint: You may use the result \(n(n+1)\), is even for \(n\), an integer.)

  8. Prove by induction that \(7\) divides \(2^{4n+2} + 3^{2n+1}\) for all nonnegative integers \(n\).

  9. Prove that for any \(n ≥ 1\) and \(x ≥ 0\) that \(\left(1+x\right)^n\geq1+nx\).

  10. For all \(n ≥ 5\), prove that \( 2^n>n^2\).

  11. For all \(n ≥ 5\), prove that \( 2^n>n^2\).

  12. Graph \(n!\) and \(2^n\), and then prove by induction that \( n! > 2^n\), for \(n>3\).

  13. Graph \(n^3\) and \(5n+12\), and then use your graph to find an appropriate \(N \in \mathbb{Z}\) to prove by induction that \( n^3 > 5n+12\) whenever \(n>N\).

  14. Prove by induction that a set \(A\) with cardinality \(|A|=n\) has \(2^n\) subsets.

  15. Prove by induction that there are \(3^n\) numbers in base 3 (using the digits 0 ,1, 2) made up of \(n\) digits.

  16. Prove by induction that there are \(4^n\) numbers in base 4 (using the digits 0 ,1, 2, 3,) made up of \(n\) digits.

  17. State the principle of mathematical induction using a conditional logical statement.

  18. Consider the sequence defined recursively as \(a_1=1,a_2=5,\) and \(a_n=5a_{n-1}-6a_{n-2}.\)

    1. Calculate the first eight terms of the recursive sequence.

    2. Prove by induction that the recursive sequence is given by the formula \(a_n=3^n-2^n.\)

  19. Consider the sequence defined recursively as \(a_1=1\) and \(a_n=2a_{n-1}+n\).

    1. Calculate the first eight terms of the recursive sequence

    2. Prove by induction that the recursive sequence is given by the formula \(a_n={4\cdot2}^{n-1}-n-1\).

  20. Prove by induction that the sum of the first \(n\) Fibonacci numbers is \[ f_1+f_2+\ldots+f_n=\sum_{i=1}^{n}{f_i=f_{n+2}-1}. \]

  21. Prove by induction that the sum of the squares of the first \(n\), Fibonacci numbers is \[ f_1^2+f_2^2+ \cdots + f_n^2 = \sum_{i=1}^{n} f_i^2=f_n \cdot\ f_{n+1}. \]