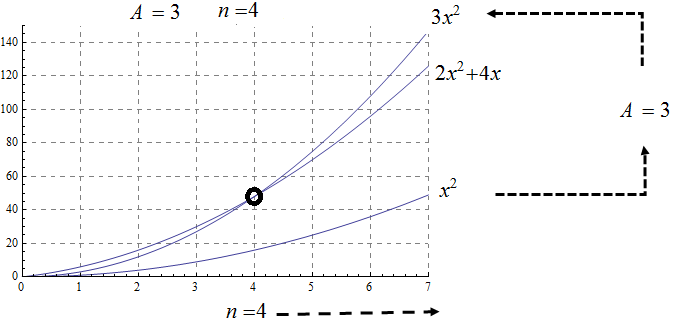7. Growth of Functions
7.1. Introducing Big O
Computer programmers are often concerned with two questions:
a) How much time does an algorithm need to complete?
b) How much memory does an algorithm need for its computation?
Big O notation is a standard way mathematicians and computer scientists use to describe how much time and how much memory is required for an algorithm to run
Big O is typically used to analyze the worst case complexity of an algorithm. If, for example, \(n\) is the size of the input data, then Big O really only cares about what happens when your input data size \(n\) becomes arbitrarily large and not quite as interested in when the input is small. Mathematically, we want to speak of complexity in the asymptotic sense, when \(n\) is arbitrarily large. In this asymptotic sense of large \(n\), we may ignore constants.
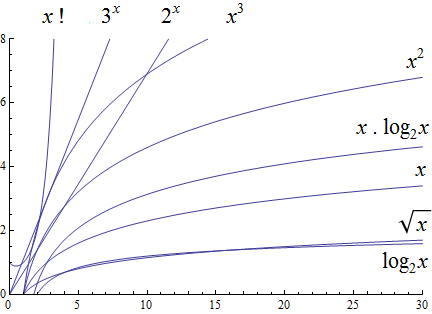
The size of the input complexities ordered from smallest to largest:
-
Constant Complexity: \(O(1)\)
-
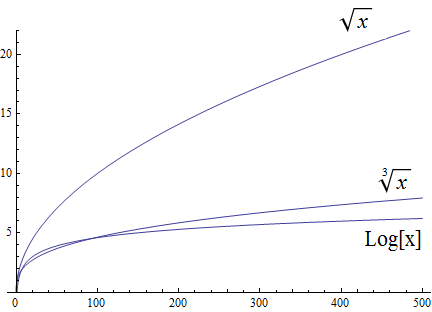
Logarithmic Complexity: \(O(\log (n))\),
-
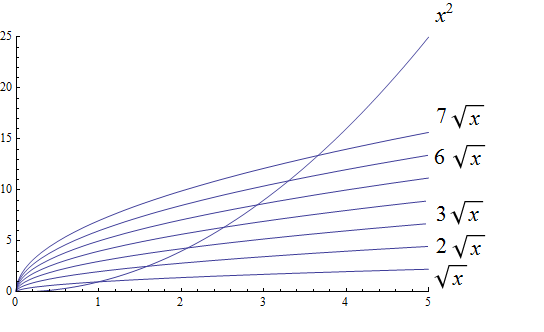
Radical complexity : \(O(\sqrt{n})\)
-
Linear Complexity: \(O(n)\)
-
Linearithmic Complexity: \(O(n\log (n))\),
-
Quadratic complexity: \(O(n^2)\)
-
Cubic complexity: \(O(n^3)\),
-
Exponential complexity: \(O(b^n)\), \( b > 1\)
-
Factorial complexity: \( O(n!)\)
Radical growth is larger than logarithmic growth:
Polynomial growth is larger than radical growth:

Exponential growth is larger than polynomial growth:
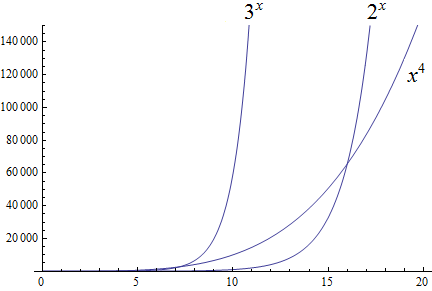
Factorial growth is larger than exponential growth:
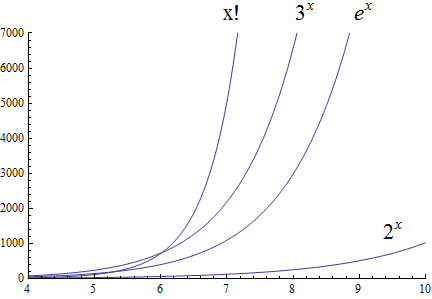
Using the graphical analysis of the growth of typical functions we have the following growth ordering, also presented graphically on a logarithmic scale graph.
The asymptotic behavior for large \(n\) should be determined by the most dominant term in the function for large \(n\). For example, \(f(x)=x^{3} + 2x^{2}-2x\) for large \(x\), is dominated by the term \(x^3\). In this case we want to state that \(O(f(x))=x^3\). For example \(f(1000) =1.001998×10^9≈ 1×10^9 =1000^3\). For large \(x\), \(f(x) ≈x^3\) or asymptotically, \(f(x)\) behaves as \(x^3\) for large \(x\). We say \(O(f(x))=x^3\) for \(f(x)=x^3 +2x^2-2x\).
Likewise we want to say that if \(c\) is a constant that \(c \cdot f(x)\), and \(f(x)\) have the same asymptotic behavior for large \(n\), or \(O(c \cdot f(x))=O(f(x))\).
Motivated by these we formally define the Big O notation.
To determine if a function \(f(x)\) is \(O(g(x))\) amounts to identifying the positive constants \(A\) and \(n\), (sometimes called witnesses). That is, we must find the factor \( A\) and the point \( k \) for which \( f(x) \leq A g(x)\), whenever \( x > k.\)
To show that a function \( f(x)\) is not \(O(g(x))\), means that no \(A\) can scale \(g(x)\) so that \( Ag(x) \geq f(x)\) for \(x\) large enough as in the following example.
7.2. Properties of Big O notation.
Suppose \(f(x)\) is \(O(F(x))\) and \(g(x)\) is \(O(G(x))\).
We can use these properties to show for instance \( 2x^2\) is \(O\left(x^2\right)\). Likewise if \(f(x) =2x^2\) and \(g(x) =4x\), then \( 2x^2\) is \(O(x^2)\) and \( 4x\) is \(O(x)\), and the maximum gives that \(2x^2+4x\) is \( O(\max(x^2, x)) =O(x^2)\).
It is true in general that if a polynomial \(f(x)\) has degree \(n\) then \(f(x)\) is \(O(x^n)\).
For example, if \(f(x)= x^3+1\) being \( O(x^3)\), and \(g(x)=x^2-x\) being \(O(x^2)\), then \(f(x) \cdot g(x)\) is \(O(x^3 \cdot x^2) =O(x^5)\). This is verified explicitly by multiplying \(f(x) \cdot g(x)= (x^3+1) \cdot (x^2-x)= x^5 -x^4+x^2-x \) which clearly is \(O(x^5)\)
As a final example we consider ordering three functions by growth using the basic properties for Big O and the basic orderings.
7.3. Exercises
-
Give Big O estimates for
-
\(f\left(x\right)=4\)
-
\(f\left(x\right)=3x-2\)
-
\(f\left(x\right)=5x^6-4x^3+1\)
-
\(f\left(x\right)=2\ \ \sqrt x+5\)
-
\(f\left(x\right)=x^5+4^x\)
-
\(f\left(x\right)=x\log{x}+3x^2\)
-
\(f\left(x\right)=5{x^2e}^x+4x!\)
-
\(f\left(x\right)=\displaystyle \frac{x^6}{x^2+1}\) (Hint: Use long division.)
-
-
Give Big O estimates for
-
\(f\left(x\right)=2^5\)
-
\(f\left(x\right)=5x-2\)
-
\(f\left(x\right)=5x^8-4x^6+x^3\)
-
\(f\left(x\right)=\) \$4 root(3)(x)+3\$
-
\(f\left(x\right)=3^x+4^x\)
-
\(f\left(x\right)=x^2\log{x}+5x^3\)
-
\(f\left(x\right)=5{x^610}^x+4x!\)
-
\(f\left(x\right)=\displaystyle \frac{x^5+2x^4-x+2}{x+2}\) (Hint: Use long division.)
-
-
Show, using the definition, that \(f\left(x\right)=3x^2+5x\) is \(O(x^2)\) with \(A=4\) and \(n=5\). Support your answer graphically.
-
Show, using the definition, that \(f\left(x\right)=x^2+6x+2\) is \(O(x^2)\) with \(A=3\) and \(n=6\). Support your answer graphically.
-
Show, using the definition, that \(f\left(x\right)=2x^3+6x^2+3\) is \(O(x^2)\). State witnesses \(A\) and \(n\), and support your answer graphically.
-
Show, using the definition, that \(f\left(x\right)=\ {3x}^3+10x^2+1000\) is \(O(x^2)\). State the witnesses \(A\) and \(n\), and support your answer graphically.
-
Show that \(f\left(x\right)=\sqrt x\) is \(O\left(x^3\right)\), but \(g\left(x\right)=x^3\) is not\(\ O(\ \sqrt x)\).
-
Show that \(f\left(x\right)= x^2\) is \(O\left(x^3\right)\), but \(g\left(x\right)=x^3\) is not\(\ O( x^2)\).
-
Show that \(f\left(x\right)=\sqrt x\) is \(O\left(x\right)\), but \(g\left(x\right)=x\) is not\(\ O(\ \sqrt x)\).
-
Show that \(f\left(x\right)=\) \$root(3)(x)\$ is \(O\left(x^2\right)\), but \(g\left(x\right)=x^2\) is not \$O( root(3)(x))\$
-
Show that \(f\left(x\right)=\) \$root(3)(x)\$ is \(O\left(x\right)\), but \(g\left(x\right)=x\) is not \$root(3)(x)\$.
-
Order the following functions by growth \(x^\frac{7}{3},\ e^x,\ 2^x,\ x^5,\ 5x+3,\ 10x^2+5x+2,\ x^3,\log{x,\ x^3\log{x}}\)
-
Order the following functions by growth from slowest to fastest. \(\ 3x!,\ {10}^x,\ x\cdot\log{x},\ \log{x\cdot\log{x,\ \ }2x^2+5x+1,\ \pi^x,x^\frac{3}{2}\ },\ 4^5,\ \ \sqrt{x\ }\cdot\log{x}\)
-
Consider the functions \(f\left(x\right)=2^x+2x^3+e^x\log{x}\) and \(g\left(x\right)=\sqrt x+x\log{x}\). Find the best big \(O\) estimates of
-
\((f+g)(x)\)
-
\((f\cdot\ g)(x)\)
-
-
Consider the functions \(f\left(x\right)=2x+3x^3+5\log{x}\) and \(g\left(x\right)=\sqrt x+x^2\log{x}\). Find the best big \(O\) estimates of
-
\((f+g)(x)\)
-
\((f\cdot\ g)(x)\)
-
-
State the definition of "\( f(x)\) is \( O(g(x))\)"" using logical quantifiers and witnesses \(A\) and \(n\).
-
Negate the definition of "\( f(x)\) is \( O(g(x))\)" using logical quantifiers, and then state in words what it means that \( f(x)\) is not \( O(g(x))\).