GGC

6. Functions

A function , written \(f : A \rightarrow B\), is a mathematical relation where each element of a set \(A\), called the domain , is associated with a unique element of another set \(B\), called the codomain of the function.

For each element \(a \in A\), we associate a unique element \(b \in B\). The set of all such associations is called a function \(f\) from \(A\) into \(B\), denoted \(f : A \rightarrow B\), with \((a,b)\) used to indicate the mapping \(f: a \rightarrow b\), or \(f(a)=b\). Here \(b\) is understood to be the image of \(a\) assigned by \(f\). The range is the set of all image values \(f(a)\). With this notation, \(a\) is allowed to vary over all elements in the set \(A\).

6.1. Injective Surjective, Bijective and Inverse Functions

A function \(f\) is injective , or one to one , if every element in the range \(B\) is associated with a unique element from the domain \(A\). This means that if \(f(m)=b\) and \(f(n)=b\), then necessarily \(m=n\).

Real-valued functions, \(f: \mathbb{R} \rightarrow \mathbb{R}\), that are strictly increasing or strictly decreasing, such as exponential or logarithmic functions, are injective.

Theorem on real valued functions

A real-valued function, \(f: \mathbb{R} \rightarrow \mathbb{R}\), that is strictly increasing or strictly decreasing is injective.

Informally a function is injective if different elements in the domain are mapped to different elements in the range. A function is not injective if at least two different elements are mapped to the same element in the range.

On a Cartesian plane, this means that every horizontal line intersects the graph at most once for an injective function. A function is not injective if at least one horizontal line intersects the graph more than once .

A function \(f\) from the set \(A\) to the set \(B\) is surjective , or onto , if the image set of \(A\) is the entire set \(B\). This means than for any element \(b \in B\) there is some element \(a \in A\) with \(f(a)=b\).

Informally a function is surjective to its codomain \(B\), if every element in \(B\) can be reached by \(f\). A function is not surjective to its codomain if at least one element in the co-domain is not in the range or in the image set of \(f\).

On a Cartesian plane, this means that every horizontal line intersects the graph at least once for a surjective function. A function is not surjective if there is a horizontal line that does not intersect the graph.

Example 1 - injective but not surjective.

Explain why the real-valued exponential function \(f(x)=2^x\) is injective, but not surjective, from \(f: \mathbb{R} \rightarrow \mathbb{R}\).

Solution

For injectivity, notice that the exponential function \(f(x)=2^x\) is strictly increasing, as can be seen from its graph. Every horizontal line intersects the graph at most once, meaning that if \(2^m =2^n\), then necessarily \(m=n\).

For surjectivity, notice that \(f(x)=2^x\), is strictly positive \((0,\infty)\) so its range is not all real numbers. As a specific, example, there is no real \(x\), for which \(f(x) = 2^x =-1\). The \(y-\) value \(y=-1\) is not reached by any real \(x\). We conclude that \(f(x)=2^x\), with \(f: \mathbb{R} \rightarrow \mathbb{R}\), is injective, but not surjective, from \(\mathbb{R} \rightarrow \mathbb{R}\).

Example 2- neither injective nor surjective

Explain why the real-valued exponential function \(f(x)=x^2\) is neither injective nor surjective, from \(f: \mathbb{R} \rightarrow \mathbb{R}\).

Solution

Notice from the graph of \(f(x)=x^2\), that the range is only non-negative numbers. This means that negative numbers cannot be reached. The function \(f(x)=x^2\) is not surjective, from \(f: \mathbb{R} \rightarrow \mathbb{R}\). In particular there is no real, \(x\), for which, for example, \(f(x)=x^2 =-1\).

Also notice that \(f(2)=4\), and \(f(-2)=4\), but \(2 \neq -2\), which means the function is not injective. A horizontal line at \(y=4\), meets the graph at both \(x=2\), and \(x=-2\).

A function \(f\) is bijective if it is both injective and surjective.

Example 3 - A bijective function

Explain why the function \(f(x)=x^3\), from \(f:R\rightarrow R\), is bijective.

Solution

We need to show that the function is both injective and surjective. Notice from the graph of \(f(x)=x^3\) that the domain and codomain are both all real numbers, \(\mathbb{R}\). Every real number \(b\) can be reached because \(f(x)=x^3 =b\), has \$x=root(3)(b)\$. For example \(-27\) is mapped to by \(-3\), because \(f(-3)=(-3)^3 = -27\), and \(64\), is mapped to by \(4\) because \(f(4)=(4)^3 = 64\). This may also be confirmed from the graph of \(f(x)=x^3\), by noticing that every horizontal line meets the graph at least once.

For injectivity, notice that the graph of \(f(x)=x^3\), that the function is strictly increasing. This means that if \(a^3=b^3\), then necessarily \(a=b\). In fact if \(a^3=b^3=c\), then, \(a=b=\) \$ root(3)(c)\$, uniquely.

Example 4 - Verifying a function is bijective

Verify that the function \(f\left(x\right)=3x+5\), from \(f:R\rightarrow R\), is bijective.

Solution

For injectivity, suppose \(f\left(m\right)=f(n)\). We want to show \(m=n\).

\(f\left(m\right)=f(n)\)

\(3m+5=3n+5\)

Subtracting 5 from both sides gives \(3m=3n\), and then multiplying both sides by \(\frac{1}{3}\) gives \(m=n\).

To show that \(f\left(x\right)\) is surjective we need to show that any \(c\in R\) can be reached by \(f\left(x\right)\). Specifically, to show that \(f\left(x\right)\) is surjective, we need to show that for any \(c\in R\), there is a corresponding \(x\) for which \(f\left(x\right)=c\). To show this consider \(f\left(x\right)=3x+5\). Equate to \(c\) and solve for \(x\).

\(f\left(x\right)=3x+5=c\)

Well, \(3x+5=c\) gives \(3x=c-5\) or \( x=\frac{c-5}{3}\). So, for any \(c\), there is an \(x\), namely \(x=\frac{c-5}{3}\), for which \(f\left(x\right)=c\).

A function \(f\) is invertible if the inverse of relation \(f : A \rightarrow B\) is also a function. The inverse is usually denoted \( f^{-1}\). For example if \((a,b)\), corresponds to \(f(a)=b\) , then \( f^{-1}: B \rightarrow A\), corresponds to \( f^{-1}(b)=a\).

The following theorem shows that invertibility of a function is equivalent to bijectivity, or a function being both a one-to one function and onto function.

Theorem on Invertibility

A function \(f: A \rightarrow B\) is invertible if and only if \(f\) is bijective.

Being able to solve an equation, amounts to being able to invert a function. Notationally, solving \(f(x) =b\) means solving for \(x\).

Using inverses \(f(x) =b\) is solved \(x=f^{-1}\left(b\right)\).

Consider, for example, \(f\left(x\right)=x^3\) we know

\$ f^{\left(-1\right)}\left(x\right)=root(3)(x)\$

Solving \(f\left(x\right)=2\) means solving \(x^3=2\). To solve \(f\left(x\right)=2\), we use \(x=f^{-1}\left(8\right)\), which in this case means,

\$ x=f^{-1}\left(8\right)=root(3)(8) = 2\$

An easy check \( f\left(2\right)=2^3=8\) and

\$ f^{-1}\left(8\right)=root(3)(8) = 2\$

Functions can, in many cases, be visualized graphically. For example when mapping from the real line \(\mathbb{R}\) to the real line such maps are viewed on a Cartesian plane.

In Appendix 1, we present several standard functions and their graphs to illustrate the important concepts of functions, including domain, codomain, range, and invertibility.

6.2. The Ceiling, Floor, Maximum and Minimum Functions

There are two important rounding functions, the ceiling function and the floor function. In discrete math often we need to round a real number to a discrete integer.

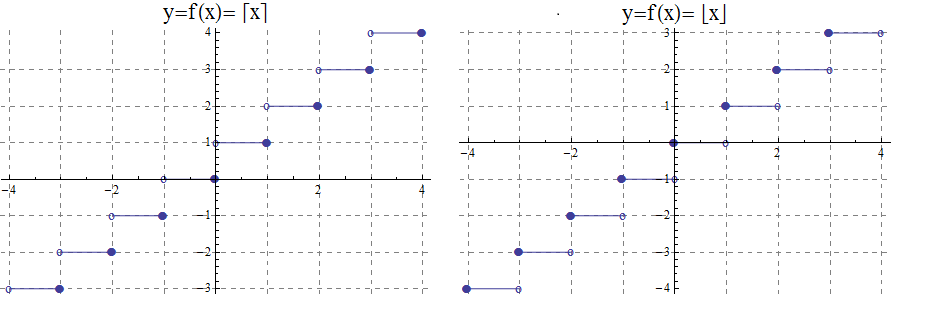
6.2.1. The Ceiling Function

The ceiling, \(f(x)=\lceil x\rceil\), function rounds up \(x\) to the nearest integer.

The ceiling function , used to compute the ceiling of \(x\), denoted, \( f(x)=\lceil x \rceil \) gives the smallest integer greater than or equal to \(x\).

For example, \( \lceil 3.4 \rceil =4\) and \( \lceil 3.7 \rceil =4\).

6.2.2. The Floor Function

The floor \( f(x)=\lfloor x \rfloor \), rounds down \(x\) to the nearest integer.

The floor function , used to compute the floor of \(x\), denoted \( f(x)=\lfloor x \rfloor \), gives the greatest integer less than or equal to \(x\).

For example,\( \lfloor 3.4 \rfloor =3\) and \( \lfloor 3.7 \rfloor =3\).

The graphs of the ceiling (\( \lceil x\rceil\))and floor (\( \lfloor x \rfloor \)) functions are shown below.

Graphs of the ceiling and floor functions,
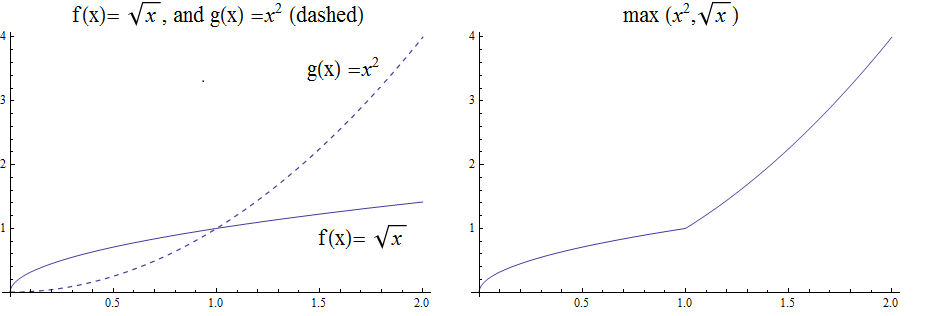
geometricsequence
Example 5

Explain why the floor function, \( f(x)=\lfloor x \rfloor \), from the real line to the set of all integers, is surjective but not injective.

Solution

For surjectivity, notice that the range, and co-domain is, \(\mathbb{Z}\), the set of all real numbers. Also for any integer, \(m\), \( f(m)=\lfloor m \rfloor =m\), meaning that every integer, \(m\), is reached, or obtained by the floor function, \( f(x)=\lfloor x \rfloor \).

For injectivity, notice that multiple numbers are rounded down to the same integer. For example, \( f(3.4)=\lfloor 3.4 \rfloor =3 \), and \( f(3.7)=\lfloor 3.7 \rfloor =3 \), so that \(f(3.4)=f(3.7)\), but \(3.4 \neq 3.7\)

6.2.3. The Max Function

The function \(h\left(x\right)=\max{\left(f\left(x\right)\right)},\ g(x))\) is evaluated at each \(x\) for which both \(f(x)\) and \(g(x)\) are defined by the function

\( h(x) =\max(f(x),g(x)) = \left\{ \begin{array}{c} f(x) \\ g(x) \end{array} \right. \begin{array}{c} \text{if } f(x)\text{ }\geq g(x) \\ \text{if } f(x) < g(x) \end{array} \)

So for example if \(f(x) =\ \sqrt x\), and \(g(x) =x^2\) then \(h(x)=\max(f(x),g(x))\), has \(h(1/4) =\max\) \( \left(\sqrt{\frac{1}{4}},\ \left(\frac{1}{4}\right)^2\right) \) \(=max\left(\frac{1}{2},\frac{1}{16}\right)=\frac{1}{2}\), and \(h(4) =\max\) \(\left(\sqrt4,\ 4^2\right)=\max(2,16)=16\). The graph of \(h(x) =\max(\sqrt x,\ x^2)\) over the interval \((0,2)\) is shown below.

Graph of \(h(x) =max(\sqrt x,\ x^2)\) over the interval \([0,2 \)]
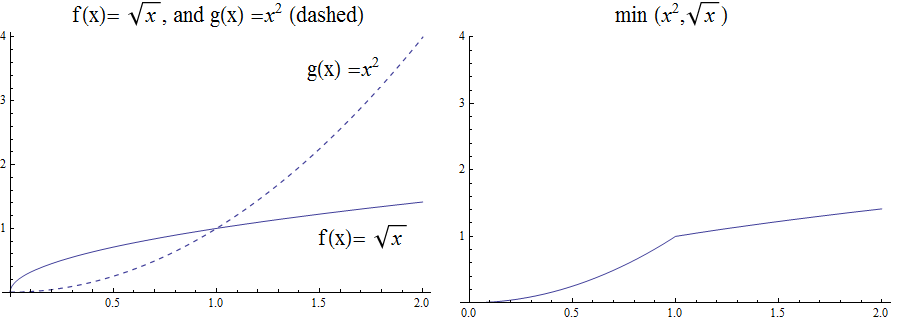
geometricsequence

6.2.4. The Min Function

The function \(h(x) =\min(f(x),g(x))\) is evaluated at each \(x\) for which both \(f(x)\) and \(g(x)\) are defined and is similar to the \(max\) function, but is defined by the minimum of \(f(x)\), and \(g(x)\) at each \(x\).

\( h(x) =\min(f(x),g(x)) = \left\{ \begin{array}{c} f(x) \\ g(x) \end{array} \right. \begin{array}{c} \text{if } f(x)\text{ }\leq g(x) \\ \text{if } f(x) > g(x) \end{array} \)

So for example if \(f(x) =\ \sqrt x\), and \(g(x) =x^2\) then \(h(x)=\min(f(x),g(x))\), has \(h(1/4) =\min\) \( \left(\sqrt{\frac{1}{4}},\ \left(\frac{1}{4}\right)^2\right) \) \(=\min\left(\frac{1}{2},\frac{1}{16}\right)=\frac{1}{16}\), and \(h(4) =\min\) \(\left(\sqrt4,\ 4^2\right)=\min(2,16)=2\).

The graph of \(h(x) =min(\sqrt x,\ x^2)\) over the interval \([0,2 \)], is shown below

Graph of \(h(x) =min(\sqrt x,\ x^2)\) over the interval \([0,2 \)]
geometricsequence

6.3. The Algebra of Functions

If two functions \(f\left(x\right)\) and \(g\left(x\right)\) have the same domain \(A\), then we can combine these functions using the common algebraic operations of addition, subtraction, multiplication, and division.

The Algebra of Functions

  1. \(\left(f+g\right)\left(x\right)=f\left(x\right)+g\left(x\right)\)

  2. \(\left(f-g\right)\left(x\right)=f\left(x\right)-g\left(x\right)\)

  3. \(\left(f\cdot\ g\right)\left(x\right)=f\left(x\right)\cdot\ g\left(x\right)\)

  4. \(\left(\frac{f}{g}\right)\left(x\right)=\frac{f\left(x\right)}{g\left(x\right)},\ \ g\left(x\right)\neq0\)

Example 6

Consider \(f\left(x\right)=x^2+1\) and \(g\left(x\right)=\sqrt x\) defined on \(f,\ g:R\rightarrow R\).Form \(\left(f+g\right)\), \(\left(f-g\right)\), \(\left(f\cdot\ g\right)\), and \(\left(\frac{f}{g}\right)\), and determine their respective domains.

Solution

The common domain is \(\ x\ \geq0\), since the square root is real valued only for \(\ x\ \geq0\).

\(\left(f+g\right)\left(x\right)=f\left(x\right)+g\left(x\right)=x^2+1+\sqrt x\) , for \( x ≥ 0\)

\(\left(f-g\right)\left(x\right)=f\left(x\right)-g\left(x\right)=x^2+1- \sqrt x\) , for \( x ≥ 0\)

\(\left(f\cdot\ g\right)\left(x\right)=f\left(x\right)\cdot\ g\left(x\right)=\left(x^2+1\right)\cdot\ \sqrt x\), for \( x ≥ 0\)

\(\left(\frac{f}{g}\right)\left(x\right)=\frac{f\left(x\right)}{g\left(x\right)}=\frac{x^2+1\cdot\ }{\ \sqrt x}\), for \( x > 0\).

Notice that the domain of \(\frac{f}{g}\) is \(x>0\), because \(g\left(0\right)=\sqrt0=0\), and division by \(0\) is not defined.

6.4. Composition of Functions

Suppose \(g:A\rightarrow B\) and \(f:B\rightarrow C\), then the functions \( f\) and \(g\), can be composed to obtain a function \(h:A\rightarrow C\), denoted as follows,

\(h\left(x\right)=\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)\) provided \(x\ \in\ A\) and \(g\left(x\right)\in B\).

Example 7

Consider \(f\left(x\right)=\frac{1}{x}\) and \(g\left(x\right)=2x-3\), defined on \(f,g:R\rightarrow R\). Notice that \(g\left(x\right)\) is defined for all real \(x\) and \(f\left(x\right)\) is defined for all real \(x\ \neq0\). Form the compositions, \(h\left(x\right)=\left(f \circ g\right)\left(x\right)\), and \(h\left(x\right)=\left(g \circ f\right)\left(x\right)\). Also determine their respective domains.

Solution

\(h\left(x\right)=\left(f \circ g\right)\left(x\right)=f\left(g\left(x\right)\right)=f\left(2x-3\right)=\frac{1}{2x-3}\). Here \(x\) needs to be in the domain of \(g\left(x\right)\), or all real \(x\), and \(g\left(x\right)\) needs to be in the domain of \(f\left(x\right)\). In particular \(g\left(x\right)\neq 0\), or \(2x-3\ \neq 0\), or \(x\ \neq\frac{3}{2}\).

By contrast, \(h\left(x\right)=\left(g\circ f\right)\left(x\right)=g\left(f\left(x\right)\right)=g\left(\frac{1}{x}\right)=2\left(\frac{1}{x}\right)-3=\frac{2}{x}-3\). Here \(x\) needs to be in the domain of \(f\left(x\right)\), or \(x\ \neq 0\), and \(f\left(x\right)\) needs to be in the domain of \(g\left(x\right)\), or \(f\left(x\right)\) can be any real number.

Example 8 - composing inverse functions

Consider \(f\left(x\right)=x^3+1\) and \$g(x) =root(3)(x-1)\$ defined on on \(f,g:R\rightarrow R\). Show that \(\left(g \circ f\right)\left(1\right)=1, \left(g \circ f\right)\left(2\right)=2, \left(g\circ f\right)\left(3\right)=3\), and \(\left(g\circ f\right)\left(x\right)=x\)

Solution

\(f\left(1\right)=1^3+1=2\)

\(f\left(2\right)=2^3+1=9\)

\(f\left(3\right)=3^3+1=28\)

\(f\left(x\right)=x^3+1\)

Therefore,

\( \left(g\circ f\right)\left(1\right)=g\left(f\left(1\right)\right)=g\left(2\right)=\) \$ root(3)(2-1)= root(3)(1)=1\$

\(\left(g\circ f\right)\left(2\right)=g\left(f\left(2\right)\right)=g\left(9\right)=\) \$ root(3)(9-1)= root(3)(8)=2\$

\(\left(g\circ f\right)\left(3\right)=g\left(f\left(3\right)\right)=g\left(28\right)=\) \$ root(3)(28-1)= root(3)(27)=3\$

\(\left(g\circ f\right)\left(x\right)=g\left(f\left(x\right)\right)=g\left(x^3+1\ \right)=\)\$ root(3)(x^3 +1 -1)= root(3)(x^3 )=x\$

Notice, in the last example, that \(g\left(x\right)\) undoes \(f\left(x\right)\), in the following sense:

\(f:1\rightarrow 2\) and \(g:2\rightarrow 1\), or the ordered pair \(\left(1,2\right)\) in \(f\), corresponds to \(\left(2,1\right)\) for \(g\).

\(f:2\rightarrow 9\) and \(g:9\rightarrow 2\), or the ordered pair \(\left(2,9\right)\), in \(f\), corresponds to \(\left(9,2\right)\) for \(g\).

\(f:3\rightarrow 28\) and \(g:28\rightarrow 3\), or the ordered pair \(\left(3,28\right)\), in \(f\), corresponds to \(\left(28,3\right)\) for \(g\).

\(f:x\rightarrow x^3+1\) and \(g:x^3+1\rightarrow x\), or the ordered pair \(\left(x,x^3+1\right)\), in \(f\), corresponds to \(\left(x^3+1,x\right)\) for \(g\).

The function \$ g(x))= root(3)(x-1) \$ is said to be the inverse of the function \(f\left(x\right)=x^3+1\). We have shown explicitly that \(\left(g\circ f\right)\left(x\right)=x\).

6.5. The Inverse of a Function

In view of this relation when composing functions that are inverses of each other, we provide an intuitive definition of inverse functions.

Suppose \(f\left(a\right):A\rightarrow B\) is bijective, then the inverse of \(f\left(x\right)\), is the function denoted \(f^{-1}\left(b\right):B\rightarrow A\).

The inverse can be similarly defined for relations in general, however the bijective property is used to ensure that the inverse of a function \(f\) is also a function.

For example the following relations have inverses as given.

\(\left\{\left(-3,\ 9\right),\ \left(-2,4\right),\ \left(-1,1\right),\ \left(0,0\right),\ \left(1,\ 1\right),\ \left(2,\ 4\right),\ \left(3,9\right)\right\}\) with inverse,

\(\left \{ \left(9,-3\ \right),\ \left(4,\ -2\ \right),\ \left(1,\ -1\right),\ \left(0,0\right),\ (1,\ 1,\ \left(4,2,\right),\ (9,3)\right \}\)

Notice that the original relation can be considered a function with domain \(A=\left\{-3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\right\}\) and co-domain \(B=\left\{0,\ 1,\ 4,\ 9\right\}\). However the inverse mapping from domain \(A=\left\{0,\ 1,\ 4,\ 9\right\}\) with co-domain \(B=\left\{-3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\right\}\), is a relation that is not a function because of the mappings \(\left(-9,3\right)\), and \(\left(-9,\ 3\right)\).

Example 9 - finding an inverse

Find the inverse \(g\left(x\right)\) of the bijective function \(f\left(x\right)=3x+5\) for \(f,\ g:R\rightarrow R\) . Verify the inverse and show \(\left(f \circ g\right)\left(x\right)=x=\left(g \circ f\right)\left(x\right)\).

Show specifically that \(f\left(2\right)=11\), and \(g\left(11\right)=2\).

Solution

If \(f:x\rightarrow y\) corresponds to \((x,y)\), then the inverse \(g:y\rightarrow x\) corresponds to \((y,x)\). This means that the inverse of the relation \(y=f\left(x\right)=3x+5\), is the relation \(x=f\left(y\right)=3y+5\).

Solving for \(y\) in \(x=f\left(y\right)\), gives \(f^{-1}(x)=y\). Solving for \(y\) in \(x=f\left(y\right)=3y+5\), gives \(x-5=3y\) or \(\frac{x-5}{3}=y=\ f^{-1}(x)=g(x)\).

We now verify that \(\left(f\circ g\right)\left(x\right)=x=\left(g \circ f\right)\left(x\right)\).

\(\left(f\circ g\right)\left(x\right)=f\left(\frac{x-5}{3}\right)=\ 3\left(\frac{x-5}{3}\right)+5=\left(x-5\right)+5=x\),

and \(\left(g \circ f\right)\left(x\right)=g\left(3x+5\right)=\ \frac{(3x+5)-5}{3}=\frac{3x+5-5}{3}=\frac{3x}{3}=x\).

Finally \(f\left(x\right)=3x+5\), and \(f\left(2\right)=3\left(2\right)+5=6+5=11\), or \(f:2\rightarrow 11\)

and \(g\left(x\right)=\frac{x-5}{3}\) and , \(g\left(11\right)=\frac{11-5}{3}=\frac{6}{3}=2\) or \(g:11\rightarrow 2\).

6.6. Exercises

  1. What can be said about the relation \(f:A\rightarrow B\), if

    1. \(\exists z\in B\forall x\in A,f\left(x\right)\neq z\)

    2. \(\exists x,y \in A, \exists z\in B,\left(x\neq y\right)\bigwedge\left(f\left(x\right)=f\left(y\right)=z\right)\)

    3. \(\forall x,y\in A, \left(f\left(x\right)=f\left(y\right)\right)\ \rightarrow\left(x=y\right)\)

    4. \(\forall x,y\in A,\left(x\neq y\right)\rightarrow\left(f\left(x\right)\neq f\left(y\right)\right)\)

    5. \(\forall z\in B, \exists x,f\left(x\right)=z\)

    6. \(\exists x,y\in A,\left(f\left(x\right)=f\left(y\right)\right)\bigwedge\left(x\ \neq\ y\right)\)

  2. Explain why exponential function \(f(x)=2^x\) is not surjective from \(f: \mathbb{R} \rightarrow \mathbb{R}\), but is in fact a bijection from \(f: \mathbb{R} \rightarrow \mathbb{R}^+\).

  3. Explain why ceiling function $ \left \lceil x \right \rceil is not surjective from \(f: \mathbb{R} \rightarrow \mathbb{R}\), but is surjective from from \(f: \mathbb{R} \rightarrow \mathbb{Z}\).

  4. Use properties of logarithms to show that \(f\left(x\right)=2^x\) and \(g\left(x\right)=\log_2{x}\), where \(f, g: \mathbb{R} \rightarrow \mathbb{R}\), are inverses by verifying that \(f\left(g\left(x\right)\right)=g\left(f\left(x\right)\right)=x\).

  5. Use properties of logarithms to show that \(f\left(x\right)=10^x\) and \(g\left(x\right)=\log{x}\), where \(f, g: \mathbb{R} \rightarrow \mathbb{R}\), are inverses by verifying that \(f\left(g\left(x\right)\right)=g\left(f\left(x\right)\right)=x\).

  6. Show that the function \(f\left(x\right)=5x-3\), from \(f: \mathbb{R} \rightarrow \mathbb{R}\), is bijective and find its inverse.

  7. Show that the function \(f\left(x\right)=2x^3-1\), from \(f: \mathbb{R} \rightarrow \mathbb{R}\) is bijective and find its inverse.

  8. Consider the function \(f(x) = \left \lceil x \right \rceil\) where \(f:\mathbb{R}\rightarrow\mathbb{Z}\).

    1. Is the function a surjection? Explain.

    2. Is the function an injection? Explain

    3. Is the function a bijection? Explain

    4. Is the inverse mapping a function? Why or why not?

    5. Evaluate

      1. \(f\left(-2.1\right)\)

      2. \(f\left(-1.9\right)\)

      3. \(f\left(1.5\right)\)

      4. \(f\left(1.9\right)\)

      5. \(f\left(2\right)\)

      6. \(f\left(2.3\right) \)

    6. Suppose \(g\left(x\right)=2x\), with \(f\left(x\right)=\left\lceil x\right\rceil\). Evaluate the following:

      1. \(f\left(g\left(2.3\right)\right)\)

      2. \(g\left(f\left(2.3\right)\right)\)

  9. Consider the function \(f(x) = \left \lfloor x \right \rfloor\) where \(f:\mathbb{R}\rightarrow\mathbb{Z}\).

    1. Is the function a surjection? Explain.

    2. Is the function an injection? Explain

    3. Is the function a bijection? Explain

    4. Is the inverse mapping a function? Why or why not?

    5. Evaluate

      1. \(f\left(-5.1\right) \)

      2. \(f\left(-3.9\right)\)

      3. \(f\left(-3.2\right)\)

      4. \(f\left(5\right) \)_

      5. \(f\left(5.3\right)\)

    6. Suppose \(g\left(x\right)=3x\), with \(f\left(x\right)=\left\lfloor x\right\rfloor\). Evaluate the following:

      1. \(f\left(g\left(5.3\right)\right)\)

      2. \(g\left(f\left(5.3\right)\right)\)

  10. The absolute value function, denoted \(f(x)=|x|\), where \(f\left(x\right):\mathbb{R} \rightarrow \mathbb{R}\), gives the distance from \(x\) to \(0\). For example, \(f\left(2.5\right)=\left|2.5\right|=2.5\). And \(f\left(-4.5\right)=\left|-4.5\right|=4.5\). Notice that if \(x \geq 0\), then \(\left|x\right|=x\). However if \(x<0\), then \(\left|x\right|=\ -x\). We can state this using the notation for piecewise functions:

    \$f(x) = |x|={( x, if x ≥ 0),(-x,if x < 0):}\$

    1. Graph \(f\left(x\right)=|x|\), for -\(10\ \le x\ \le10\)

    2. Evaluate

      1. \(f(-5)=|-5|\),

      2. \(f(-2.5)=|-2.5|\),

      3. \(f(3.5)=|3.5|\).

    3. Show that \(f\left(x\right)=\left|x\right|\), with \(f:\mathbb{R}\rightarrow \mathbb{R}\), is not injective.

    4. Show that \(f\left(x\right)=\left|x\right|\), with \(f:\mathbb{R}\rightarrow \mathbb{R}\), is not surjective.

    5. Consider \(g\left(x\right)=3x+2\), with \(g:\mathbb{R}\rightarrow \mathbb{R}\), and \(f\left(x\right)=|x|\). Find and simplify the following:

      1. \(\left(g\circ f\right)\left(x\right)\)

      2. \(\left(f\circ g\right)\left(x\right)\)

  11. A real-valued function, \(f: \mathbb{R} \rightarrow \mathbb{R}\), is said to be strictly increasing if whenever \$x<y\$, then \$f(x)<f(y)\$.

    1. State this using logical quantifiers.

    2. State a similar definition for a strictly decreasing function, and then translate using logical quantifiers.